
Finite Dimensional Subspace of a Normed linear space is closed || Functional analysis in telugu || - YouTube
Honors Analysis - Homework 5 1. Let V be a Banach space, and W ⊂ V a closed subspace. Show that the quotient space V/W is also

linear algebra - Does $V=W\oplus W^\perp$ hold when $W$ is infinitely- dimensional? - Mathematics Stack Exchange

If Y Is A Proper Finite Dimensional Subspace of Normed Space X, Then Dist (X, Y) 1 | PDF | Derivative | Functional Analysis

real analysis - Show that S is non-compact and deduce further that the closed unit ball in X is non-compact. - Mathematics Stack Exchange

2017-2018 Example Sheet 1 - Mich 2017 FUNCTIONAL ANALYSIS – EXAMPLES 1 AZ LetXbe a normed space. - Studocu

SOLVED: Let X be a closed subspace and Y be a finite dimensional subspace of a normed space X. Then X+Y is closed in X. Hint: Proof of 5.4b





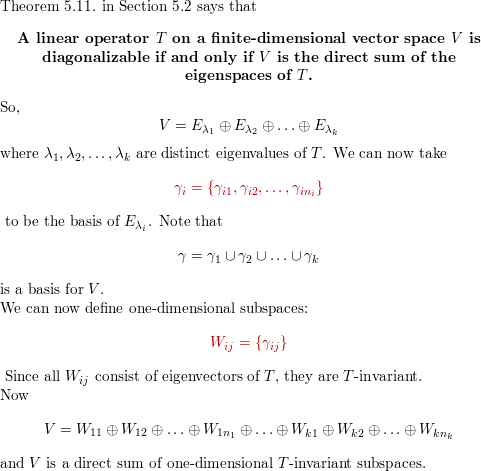


![ANSWERED] Let X₁ be a closed subspace and X₂ be a finite dimen... - Algebra - Kunduz ANSWERED] Let X₁ be a closed subspace and X₂ be a finite dimen... - Algebra - Kunduz](https://media.kunduz.com/media/sug-question/raw/79397977-1659890173.8687193.jpeg)







